TERCEIRA QUANTIZAÇÃO E RELATIVIDADE SDCTIE GRACELI EM
Onda estacionária
TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI
TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.
FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x [EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG
XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli + DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
número atômico, estrutura eletrônica, níveis de energia - TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- T l T l E l Fl dfG l
X [ESTADO QUÂNTICO]
Ondas estacionárias são ondas que possuem um padrão de vibração estacionário. Formam-se a partir de uma superposição de duas ondas idênticas mas em sentidos opostos, normalmente quando as ondas estão confinadas no espaço como ondas sonoras em um tubo fechado e ondas de uma corda com as extremidades fixas. Esse tipo de onda é caracterizado por pontos fixos de valor zero, chamados de nodos, e pontos de máximo também fixos, chamados de antinodos. São ondas resultantes da superposição de duas ondas de mesma frequência, mesma amplitude, mesmo comprimento de onda, mesma direção e sentidos opostos. [1]
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Ondas estacionárias são ondas que possuem um padrão de vibração estacionário. Formam-se a partir de uma superposição de duas ondas idênticas mas em sentidos opostos, normalmente quando as ondas estão confinadas no espaço como ondas sonoras em um tubo fechado e ondas de uma corda com as extremidades fixas. Esse tipo de onda é caracterizado por pontos fixos de valor zero, chamados de nodos, e pontos de máximo também fixos, chamados de antinodos. São ondas resultantes da superposição de duas ondas de mesma frequência, mesma amplitude, mesmo comprimento de onda, mesma direção e sentidos opostos. [1]
Ondas Opostas[editar | editar código-fonte]
Uma onda estacionária em uma linha de transmissão é uma onda na qual a distribuição de corrente elétrica, tensão elétrica, ou campo elétrico é formado pela superposição de duas ondas de mesma frequência se propagando em sentidos opostos. O efeito é uma série de nodos (deslocamento zero) e antinodos (deslocamento máximo) em pontos fixos ao longo da linha de transmissão. Esta onda estacionária pode ser formada quando uma onda é transmitida a partir de uma extremidade da linha de transmissão e é refletida na outra extremidade por um casamento de impedâncias, ex., descontinuidade, como um circuito aberto ou um curto-circuito.[2]
Na prática, perdas na linha de transmissão e outros componentes significa uma reflexão perfeita e uma onda estacionária pura nunca é gerada. O resultado é uma onda estacionária parcial, que é uma superposição de uma onda estacionária e uma outra onda. A forma de onda resultante é medida pela relação de ondas estacionárias (ROE).[3]
Uma onda estacionária em uma linha de transmissão é uma onda na qual a distribuição de corrente elétrica, tensão elétrica, ou campo elétrico é formado pela superposição de duas ondas de mesma frequência se propagando em sentidos opostos. O efeito é uma série de nodos (deslocamento zero) e antinodos (deslocamento máximo) em pontos fixos ao longo da linha de transmissão. Esta onda estacionária pode ser formada quando uma onda é transmitida a partir de uma extremidade da linha de transmissão e é refletida na outra extremidade por um casamento de impedâncias, ex., descontinuidade, como um circuito aberto ou um curto-circuito.[2]
Na prática, perdas na linha de transmissão e outros componentes significa uma reflexão perfeita e uma onda estacionária pura nunca é gerada. O resultado é uma onda estacionária parcial, que é uma superposição de uma onda estacionária e uma outra onda. A forma de onda resultante é medida pela relação de ondas estacionárias (ROE).[3]
Descrição Matemática[editar | editar código-fonte]
Quando há um movimento oscilatório harmônico simples, como por exemplo em uma corda, o deslocamento de cada ponto da onda pode ser descrito pela equação:
- X
Quando há um movimento oscilatório harmônico simples, como por exemplo em uma corda, o deslocamento de cada ponto da onda pode ser descrito pela equação:
- X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
Sendo:
- An (x) a amplitude, que depende da posição x do elemento,
- ω a frequência angular (medida em radianos por segundo),
- δn a constante de fase,
- t é a variável tempo.
A função An (x) é a forma da onda quando a vibração tem seu deslocamento máximo e em seu n-ésimo modo pode ser definida por:
- X
Sendo:
- An (x) a amplitude, que depende da posição x do elemento,
- ω a frequência angular (medida em radianos por segundo),
- δn a constante de fase,
- t é a variável tempo.
A função An (x) é a forma da onda quando a vibração tem seu deslocamento máximo e em seu n-ésimo modo pode ser definida por:
- X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
Onde:
- kn é o número de onda (definido por 2π/λn)
Utilizando ambas as equações podemos definir a função da onda em seu n-ésimo harmônico por:
- X
Onde:
- kn é o número de onda (definido por 2π/λn)
Utilizando ambas as equações podemos definir a função da onda em seu n-ésimo harmônico por:
- X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
Presumindo que ambas as condições necessárias para que ocorra o movimento da onda estacionária sejam satisfeitas. São elas:
Presumindo que ambas as condições necessárias para que ocorra o movimento da onda estacionária sejam satisfeitas. São elas:
Ondas Estacionárias em Cordas[editar | editar código-fonte]
Em certas frequências de oscilação cordas com uma ou ambas as extremidades fixas podem gerar ondas estacionárias.[1]
Em certas frequências de oscilação cordas com uma ou ambas as extremidades fixas podem gerar ondas estacionárias.[1]
Corda com Ambas as Extremidades Fixas[editar | editar código-fonte]
Se excitada uma corda fixa em ambas as extremidades com um movimento harmônico simples de amplitude pequena, são produzidos padrões de ondas estacionárias para certas frequências de excitação. As frequências que geram este comportamento são chamadas de frequência de ressonância. A menor frequência de ressonância é chamada de frequência fundamental (vamos chama-la de f1) e produz um padrão de onda estacionária chamado de modo fundamental ou primeiro harmônico. Cada frequência de ressonância juntamente com a respectiva função de onda corresponde a um modo de vibração. Como a corda está fixa em ambas as extremidades, nestes locais é formado um nodo. Nota-se assim que no primeiro harmônico haverá somente um antinodo, no segundo haverá dois antinodos e assim por diante. A partir destas observações e considerando λ o comprimento de onda, temos que:
- A distância entre dois nodos consecutivos, que é a mesma de dois antinodos, vale .
- A distância entre um nó e um ventre consecutivo vale .
Sendo L o comprimento da corda, ele pode ser expresso por:
- X
Se excitada uma corda fixa em ambas as extremidades com um movimento harmônico simples de amplitude pequena, são produzidos padrões de ondas estacionárias para certas frequências de excitação. As frequências que geram este comportamento são chamadas de frequência de ressonância. A menor frequência de ressonância é chamada de frequência fundamental (vamos chama-la de f1) e produz um padrão de onda estacionária chamado de modo fundamental ou primeiro harmônico. Cada frequência de ressonância juntamente com a respectiva função de onda corresponde a um modo de vibração. Como a corda está fixa em ambas as extremidades, nestes locais é formado um nodo. Nota-se assim que no primeiro harmônico haverá somente um antinodo, no segundo haverá dois antinodos e assim por diante. A partir destas observações e considerando λ o comprimento de onda, temos que:
- A distância entre dois nodos consecutivos, que é a mesma de dois antinodos, vale .
- A distância entre um nó e um ventre consecutivo vale .
Sendo L o comprimento da corda, ele pode ser expresso por:
- X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
Onde n representa o n-ésima harmônica.[1]
Onde n representa o n-ésima harmônica.[1]
Corda com Uma das Extremidades Fixa e a Outra Livre[editar | editar código-fonte]
Quando uma das extremidades se encontra fixa e a outra, por exemplo, se encontra ligada a um anel (de massa desprezível) livre para deslizar na vertical, sem atrito. Como o movimento da corda é livre na vertical, diz-se que aquela é uma extremidade livre. Como a massa do anel é desprezível, a força vertical gerada pela corda geraria uma aceleração infinita ao anel. Se a forma da corda junto ao anel permanecer horizontal a aceleração se manterá finita. Assim, na extremidade livre da corda haverá um antinodo. Deve-se notar, portanto, que diferentemente da corda fixa em ambas extremidades, a cada harmônica há um número ímpar de antinodos. Como a corda representa a distância entre um nodo (a extremidade fixa) e um antinodo (a extremidade livre), o comprimento da corda é dado por:
- X
Quando uma das extremidades se encontra fixa e a outra, por exemplo, se encontra ligada a um anel (de massa desprezível) livre para deslizar na vertical, sem atrito. Como o movimento da corda é livre na vertical, diz-se que aquela é uma extremidade livre. Como a massa do anel é desprezível, a força vertical gerada pela corda geraria uma aceleração infinita ao anel. Se a forma da corda junto ao anel permanecer horizontal a aceleração se manterá finita. Assim, na extremidade livre da corda haverá um antinodo. Deve-se notar, portanto, que diferentemente da corda fixa em ambas extremidades, a cada harmônica há um número ímpar de antinodos. Como a corda representa a distância entre um nodo (a extremidade fixa) e um antinodo (a extremidade livre), o comprimento da corda é dado por:
- X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
Onde n representa o n-ésima harmônica, não havendo os harmônicos pares nesse sistema.[1]
Onde n representa o n-ésima harmônica, não havendo os harmônicos pares nesse sistema.[1]
Ondas Sonoras Estacionárias[editar | editar código-fonte]
Tubos Sonoros[editar | editar código-fonte]
Alguns tubos sonoros contêm uma coluna de ar que pode executar uma vibração estacionária. Se as duas extremidades do tubo são desobstruídas, ele é denominado tubo aberto; chamamos de tubo fechado o tubo que tem a extremidade tapada. Como são ondas longitudinais, a construção da vibração estacionária no tubo deve obedecer às seguintes condições de contorno:
♦ as extremidades abertas são locais onde a vibração é livre, correspondendo, portanto, a ventres;
♦ as extremidades fechadas são locais onde não há vibração longitudinal; são, portanto, nós.[4]
Iremos considerar um tubo com uma extremidade aberta e a outra fechada. Como uma onda sonora pode ser considerada uma onda de pressão ou uma onda de deslocamento e as oscilações de pressão e deslocamento são desfasadas em 90º, em uma onda sonora estacionária onde há um nodo de pressão há um antinodo de deslocamento e vice-versa. Se a circunferência do tubo for muito menor que o comprimento da onda, podemos dizer que a onda sonora no tubo é unidimensional e há um nodo de pressão na extremidade aberta do tubo. Há, portanto, um antinodo na extremidade fechada do tubo. Assim as oscilações em um tubo com uma extremidade aberta e a outro fechada se assemelha com uma corda com uma extremidade fixa e a outra livre. Seguindo a mesma interpretação, em um tubo com ambas as extremidades abertas, há um nodo de pressão em cada extremidade. Estas configurações fazem com que as ondas estacionárias em um tubo de ambas as extremidades abertas se assemelhe as de uma corda com ambas as extremidades fixas.[1]
Em uma coluna de ar que esteja aberta em ambas as extremidades, no modo fundamental, o comprimento de onda é o dobro do comprimento da coluna de ar e , portanto, a frequência f1 fundamental é . De maneira similar, as frequências dos harmônicos superiores são 2f1, 3f1,... .Os harmônicos superiores são múltiplos inteiros da frequência fundamental. Como estão presentes todos os harmônicos, podemos expressar as frequências naturais de vibração como:
- X
Alguns tubos sonoros contêm uma coluna de ar que pode executar uma vibração estacionária. Se as duas extremidades do tubo são desobstruídas, ele é denominado tubo aberto; chamamos de tubo fechado o tubo que tem a extremidade tapada. Como são ondas longitudinais, a construção da vibração estacionária no tubo deve obedecer às seguintes condições de contorno:
♦ as extremidades abertas são locais onde a vibração é livre, correspondendo, portanto, a ventres;
♦ as extremidades fechadas são locais onde não há vibração longitudinal; são, portanto, nós.[4]
Iremos considerar um tubo com uma extremidade aberta e a outra fechada. Como uma onda sonora pode ser considerada uma onda de pressão ou uma onda de deslocamento e as oscilações de pressão e deslocamento são desfasadas em 90º, em uma onda sonora estacionária onde há um nodo de pressão há um antinodo de deslocamento e vice-versa. Se a circunferência do tubo for muito menor que o comprimento da onda, podemos dizer que a onda sonora no tubo é unidimensional e há um nodo de pressão na extremidade aberta do tubo. Há, portanto, um antinodo na extremidade fechada do tubo. Assim as oscilações em um tubo com uma extremidade aberta e a outro fechada se assemelha com uma corda com uma extremidade fixa e a outra livre. Seguindo a mesma interpretação, em um tubo com ambas as extremidades abertas, há um nodo de pressão em cada extremidade. Estas configurações fazem com que as ondas estacionárias em um tubo de ambas as extremidades abertas se assemelhe as de uma corda com ambas as extremidades fixas.[1]
Em uma coluna de ar que esteja aberta em ambas as extremidades, no modo fundamental, o comprimento de onda é o dobro do comprimento da coluna de ar e , portanto, a frequência f1 fundamental é . De maneira similar, as frequências dos harmônicos superiores são 2f1, 3f1,... .Os harmônicos superiores são múltiplos inteiros da frequência fundamental. Como estão presentes todos os harmônicos, podemos expressar as frequências naturais de vibração como:
- X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
Onde n representa o n-ésima harmônica, v é a velocidade do som no ar,L comprimento do tubo.
Se uma coluna de ar é fechada em uma extremidade e aberta na outra, a extremidade fechada é um nó de deslocamento. Neste caso, o comprimento de onda para o modo fundamental é quatro vezes o comprimento da coluna. Portanto, a frequência fundamental f1 é igual a e as frequências dos harmônicos superiores são iguais a 3f1, 5f1,.... Isto é, em uma coluna de ar que é fechada em uma extremidade, apenas os harmônicos ímpares estão presentes e estes são:
- X
Onde n representa o n-ésima harmônica, v é a velocidade do som no ar,L comprimento do tubo.
Se uma coluna de ar é fechada em uma extremidade e aberta na outra, a extremidade fechada é um nó de deslocamento. Neste caso, o comprimento de onda para o modo fundamental é quatro vezes o comprimento da coluna. Portanto, a frequência fundamental f1 é igual a e as frequências dos harmônicos superiores são iguais a 3f1, 5f1,.... Isto é, em uma coluna de ar que é fechada em uma extremidade, apenas os harmônicos ímpares estão presentes e estes são:
- X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
- As ondas estacionárias em colunas de ar são as fontes primárias dos sons produzidos por instrumentos de sopro. Em um instrumento de sopro de madeira, uma chave é pressionada abrindo um furo no lado da coluna. O furo define a extremidade da coluna vibrante de ar(pois age como uma extremidade aberta- a pressão pode ser liberada), de modo que a coluna de seja de fato encurtada e a frequência fundamental de eleve. Em um instrumento de metal, o comprimento da coluna de ar é mudado por uma seção ajustável, como em um trombone de vara, ou adicionando-se segmentos ao tubo, como é feito em um trompete quando uma válvula é pressionada.[5]
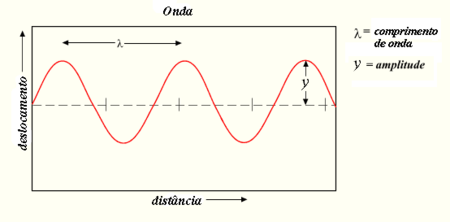
Amplitude é uma medida escalar negativa ou nula ou positiva da magnitude de oscilação temporal de uma onda, caso esta apresente alternâncias em torno do eixo [horizontal, usualmente] do tempo.
A distância Y é a amplitude da onda, também conhecida como "pico de amplitude" para diferenciar de outro conceito de amplitude, usado especialmente em engenharia elétrica: root mean square amplitude (ou amplitude rms), definida como a raiz quadrada da média temporal da distância vertical entre o gráfico e o eixo horizontal. O uso de "pico de amplitude" não é ambíguo para ondas simétricas e periódicas como senóides, onda quadrada e onda triangular. Para ondas sem simetria, como por exemplo pulsos periódicos em uma direção, o termo "pico de amplitude" torna-se ambíguo pois o valor obtido é diferente dependendo se o máximo valor positivo é medido em relação à média, se o máximo valor negativo é medido em relação à média ou se o máximo sinal positivo é medido em relação ao máximo sinal negativo e dividido por dois. Para ondas complexas, especialmente sinais sem repetição tais como ruído, a amplitude rms é usada frequentemente porque não tem essa ambiguidade e também porque tem um sentido físico. Por exemplo, a potência transmitida por uma onda acústica ou eletromagnética ou por um sinal elétrico é proporcional à raiz quadrada da amplitude rms (e em geral, não tem essa relação com a raiz do pico de amplitude)
A seguinte equação é, usualmente, adotada para apresentar o conceito de amplitude:
- y é a função de onda, que, por sinal, representa sua amplitude instantânea, num dado instante "t".
- A é a amplitude da onda.
- sen () é, nesse caso ilustrativo, o argumento representativo de uma função senoidal.
- t é o instante de tempo, variável independente.
- k é a medida de translação temporal.
- b é a medida de translação de onda.
Infinitas são as possibilidades de formulação matemática. Deve-se ter em conta que a apresentação oferecida visa apenas permitir a conexão entre a ideia de amplitude e sua correspondente formulação por meio duma sentença matemática.
A unidade utilizada para a medida depende do tipo da onda. Por exemplo, a amplitude de ondas de som e sinais de áudio costumam ser expressas em decibéis (dB). A amplitude depende do instante em que a onda é observada, já que sua propagação em meios materiais é acompanhada de amortecimento, devido à transferência de energia para o meio. [1]
A amplitude de uma onda pode ser constante ou variar com o tempo. Variações de amplitude são a base para modulações AM.
X
- As ondas estacionárias em colunas de ar são as fontes primárias dos sons produzidos por instrumentos de sopro. Em um instrumento de sopro de madeira, uma chave é pressionada abrindo um furo no lado da coluna. O furo define a extremidade da coluna vibrante de ar(pois age como uma extremidade aberta- a pressão pode ser liberada), de modo que a coluna de seja de fato encurtada e a frequência fundamental de eleve. Em um instrumento de metal, o comprimento da coluna de ar é mudado por uma seção ajustável, como em um trombone de vara, ou adicionando-se segmentos ao tubo, como é feito em um trompete quando uma válvula é pressionada.[5]
Amplitude é uma medida escalar negativa ou nula ou positiva da magnitude de oscilação temporal de uma onda, caso esta apresente alternâncias em torno do eixo [horizontal, usualmente] do tempo.
A distância Y é a amplitude da onda, também conhecida como "pico de amplitude" para diferenciar de outro conceito de amplitude, usado especialmente em engenharia elétrica: root mean square amplitude (ou amplitude rms), definida como a raiz quadrada da média temporal da distância vertical entre o gráfico e o eixo horizontal. O uso de "pico de amplitude" não é ambíguo para ondas simétricas e periódicas como senóides, onda quadrada e onda triangular. Para ondas sem simetria, como por exemplo pulsos periódicos em uma direção, o termo "pico de amplitude" torna-se ambíguo pois o valor obtido é diferente dependendo se o máximo valor positivo é medido em relação à média, se o máximo valor negativo é medido em relação à média ou se o máximo sinal positivo é medido em relação ao máximo sinal negativo e dividido por dois. Para ondas complexas, especialmente sinais sem repetição tais como ruído, a amplitude rms é usada frequentemente porque não tem essa ambiguidade e também porque tem um sentido físico. Por exemplo, a potência transmitida por uma onda acústica ou eletromagnética ou por um sinal elétrico é proporcional à raiz quadrada da amplitude rms (e em geral, não tem essa relação com a raiz do pico de amplitude)
A seguinte equação é, usualmente, adotada para apresentar o conceito de amplitude:
- y é a função de onda, que, por sinal, representa sua amplitude instantânea, num dado instante "t".
- A é a amplitude da onda.
- sen () é, nesse caso ilustrativo, o argumento representativo de uma função senoidal.
- t é o instante de tempo, variável independente.
- k é a medida de translação temporal.
- b é a medida de translação de onda.
Infinitas são as possibilidades de formulação matemática. Deve-se ter em conta que a apresentação oferecida visa apenas permitir a conexão entre a ideia de amplitude e sua correspondente formulação por meio duma sentença matemática.
A unidade utilizada para a medida depende do tipo da onda. Por exemplo, a amplitude de ondas de som e sinais de áudio costumam ser expressas em decibéis (dB). A amplitude depende do instante em que a onda é observada, já que sua propagação em meios materiais é acompanhada de amortecimento, devido à transferência de energia para o meio. [1]
A amplitude de uma onda pode ser constante ou variar com o tempo. Variações de amplitude são a base para modulações AM.
X
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS
Definição de Amplitude Modulada aceita internacionalmente[editar | editar código-fonte]
No caso de transmissão de sinais, o modelo adotado pelo Bureau of Naval Personel Training Publications Division, e seguido pelo ocidente para definir o AM, diz que a "amplitude modulada é a variação da intensidade de saída de RF (rádio frequência) do transmissor a uma velocidade de áudio". A tensão de saída do radiotransmissor tem uma variação que oscila para cima e para baixo de seu valor nominal de acordo com a frequência de áudio. (Ver exemplos demonstrados nos parágrafos abaixo).
Para áudio de alta frequência, a radiofrequência terá uma variação em amplitude mais rápida, para áudio de baixa frequência, esta variação será mais lenta. Logo, a variação da portadora de RF deve corresponder em amplitude a variação ocasionada pelo Áudio. A resultante de modulação em amplitude para uma frequência de áudio fixa pode ser separada para análise do processo em três ondas distintas cuja amplitude é constante.
O sistema de modulação em amplitude é o sistema de modulação mais antigo (1980). Existem diversos tipos de sistemas de modulação em amplitude, destacando-se: AM-DSB (Amplitude Modulation Double SideBand), AM-SSB (Amplitude Modulation Single SideBand) e AM-VSB (Amplitude Modulation Vestigial SideBand). Os sistemas anteriores ainda podem ser subdivididos em relação a existência ou não da portadora no sinal modulado: AM-DSB/SC: Amplitude Modulation Double SideBand with Supressed Carrier AM-SSB/SC: Amplitude Modulation Single SideBand with Supressed Carrier AM-VSB/SC: Amplitude Modulation Vestigial SideBand with Supressed Carrier
No caso de transmissão de sinais, o modelo adotado pelo Bureau of Naval Personel Training Publications Division, e seguido pelo ocidente para definir o AM, diz que a "amplitude modulada é a variação da intensidade de saída de RF (rádio frequência) do transmissor a uma velocidade de áudio". A tensão de saída do radiotransmissor tem uma variação que oscila para cima e para baixo de seu valor nominal de acordo com a frequência de áudio. (Ver exemplos demonstrados nos parágrafos abaixo).
Para áudio de alta frequência, a radiofrequência terá uma variação em amplitude mais rápida, para áudio de baixa frequência, esta variação será mais lenta. Logo, a variação da portadora de RF deve corresponder em amplitude a variação ocasionada pelo Áudio. A resultante de modulação em amplitude para uma frequência de áudio fixa pode ser separada para análise do processo em três ondas distintas cuja amplitude é constante.
O sistema de modulação em amplitude é o sistema de modulação mais antigo (1980). Existem diversos tipos de sistemas de modulação em amplitude, destacando-se: AM-DSB (Amplitude Modulation Double SideBand), AM-SSB (Amplitude Modulation Single SideBand) e AM-VSB (Amplitude Modulation Vestigial SideBand). Os sistemas anteriores ainda podem ser subdivididos em relação a existência ou não da portadora no sinal modulado: AM-DSB/SC: Amplitude Modulation Double SideBand with Supressed Carrier AM-SSB/SC: Amplitude Modulation Single SideBand with Supressed Carrier AM-VSB/SC: Amplitude Modulation Vestigial SideBand with Supressed Carrier
Motivação[editar | editar código-fonte]
A transmissão de rádio é feita através da difusão de ondas eletromagnéticas. Estas são transmitidas no ar mais eficientemente em altas frequências do que em baixas frequências. Isso porque, de modo geral, o tamanho da antena que deve receber um sinal de rádio é diretamente proporcional ao comprimento de onda transmitida. Se fosse desejado transmitir ondas com frequências equivalentes às frequências de voz (da ordem de 80hz a 1500Hz, segundo FOLMER-JOHNSON - 1968 e EFRON - 1969 [1]), seriam necessárias antenas de proporções gigantescas (alguns quilômetros de comprimento). Por este motivo, foi necessário encontrar alguma forma de transmitir as informações usando ondas de alta frequência.
Outra necessidade atendida pela modulação de ondas foi a necessidade de se compartilhar um meio de transmissão, no caso o ar, entre um número de transmissores. Para alcançar este objetivo, basta usar a mensagem para modular ondas de frequências diferentes. Desta forma, o receptor pode "selecionar" uma frequência para demodular retirando assim a informação apenas de um transmissor. Isto é exatamente o que fazemos quando selecionamos uma estação de rádio ou um canal de televisão.
A solução foi justamente modular as ondas de alta frequência de modo que a informação a ser transmitida esteja contida nestas ondas e possam ser transmitidas eficientemente pelo ar. Esta informação poderia ser facilmente recuperada num receptor de rádio, através de um processo chamado demodulação.
A transmissão de rádio é feita através da difusão de ondas eletromagnéticas. Estas são transmitidas no ar mais eficientemente em altas frequências do que em baixas frequências. Isso porque, de modo geral, o tamanho da antena que deve receber um sinal de rádio é diretamente proporcional ao comprimento de onda transmitida. Se fosse desejado transmitir ondas com frequências equivalentes às frequências de voz (da ordem de 80hz a 1500Hz, segundo FOLMER-JOHNSON - 1968 e EFRON - 1969 [1]), seriam necessárias antenas de proporções gigantescas (alguns quilômetros de comprimento). Por este motivo, foi necessário encontrar alguma forma de transmitir as informações usando ondas de alta frequência.
Outra necessidade atendida pela modulação de ondas foi a necessidade de se compartilhar um meio de transmissão, no caso o ar, entre um número de transmissores. Para alcançar este objetivo, basta usar a mensagem para modular ondas de frequências diferentes. Desta forma, o receptor pode "selecionar" uma frequência para demodular retirando assim a informação apenas de um transmissor. Isto é exatamente o que fazemos quando selecionamos uma estação de rádio ou um canal de televisão.
A solução foi justamente modular as ondas de alta frequência de modo que a informação a ser transmitida esteja contida nestas ondas e possam ser transmitidas eficientemente pelo ar. Esta informação poderia ser facilmente recuperada num receptor de rádio, através de um processo chamado demodulação.
Métodos de modulação[editar | editar código-fonte]
Originalmente, a modulação em amplitude era feita transmitindo-se uma portadora com uma amplitude de base e alterando-se esta amplitude em função da mensagem que queria-se transmitir. Este tipo foi chamado de modulação AM DSB-FC (double-sideband full carrier). Como será explicado a seguir, neste tipo de modulação, além da portadora são transmitidos dois outros conjuntos de frequências (espectros) chamadas de bandas laterais, nas quais está contida a mensagem a ser transmitida.
A modulação AM DSB-FC é altamente ineficiente pois a maior parte da potência gerada é usada para transmitir a portadora, e não a mensagem. Eventualmente descobriu-se que não era necessário enviar a portadora acompanhada das bandas laterais, mas era possível enviar apenas as bandas laterais, onde estava contida a mensagem, evitando assim gastos desnecessários na portadora. A esta modulação deu-se o nome de modulação AM DSB-SC (double-sideband supressed carrier) uma vez que a portadora havia sido suprimida. Este método possuía a desvantagem, no entanto, de exigir circuitos mais complexos na demodulação do sinal.
Como evolução deste último método, ficou claro que não apenas era possível enviar as bandas laterais sem a portadora, mas era possível enviar apenas uma banda, sem perda de informação. A este tipo de modulação se deu o nome de modulação AM SSB (single-sideband), por possuir apenas uma banda. Este, apesar de ser o método mais eficiente, é também o mais complexo de se modular e demodular.
Finalmente, como um compromisso entre eficiência e complexidade, foi criada a modulação AM VSB (vestigial-sideband), onde uma banda é transmitida por inteiro e a outra é parcialmente suprimida (de aí o nome vestigial).
Originalmente, a modulação em amplitude era feita transmitindo-se uma portadora com uma amplitude de base e alterando-se esta amplitude em função da mensagem que queria-se transmitir. Este tipo foi chamado de modulação AM DSB-FC (double-sideband full carrier). Como será explicado a seguir, neste tipo de modulação, além da portadora são transmitidos dois outros conjuntos de frequências (espectros) chamadas de bandas laterais, nas quais está contida a mensagem a ser transmitida.
A modulação AM DSB-FC é altamente ineficiente pois a maior parte da potência gerada é usada para transmitir a portadora, e não a mensagem. Eventualmente descobriu-se que não era necessário enviar a portadora acompanhada das bandas laterais, mas era possível enviar apenas as bandas laterais, onde estava contida a mensagem, evitando assim gastos desnecessários na portadora. A esta modulação deu-se o nome de modulação AM DSB-SC (double-sideband supressed carrier) uma vez que a portadora havia sido suprimida. Este método possuía a desvantagem, no entanto, de exigir circuitos mais complexos na demodulação do sinal.
Como evolução deste último método, ficou claro que não apenas era possível enviar as bandas laterais sem a portadora, mas era possível enviar apenas uma banda, sem perda de informação. A este tipo de modulação se deu o nome de modulação AM SSB (single-sideband), por possuir apenas uma banda. Este, apesar de ser o método mais eficiente, é também o mais complexo de se modular e demodular.
Finalmente, como um compromisso entre eficiência e complexidade, foi criada a modulação AM VSB (vestigial-sideband), onde uma banda é transmitida por inteiro e a outra é parcialmente suprimida (de aí o nome vestigial).
Forma padrão[editar | editar código-fonte]
A forma padrão de uma onda modulada em amplitude (AM) é definida como:
X
A forma padrão de uma onda modulada em amplitude (AM) é definida como:
X
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC].
 + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
 + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL ![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCK

 [ESTADO QUÂNTICO]
[ESTADO QUÂNTICO]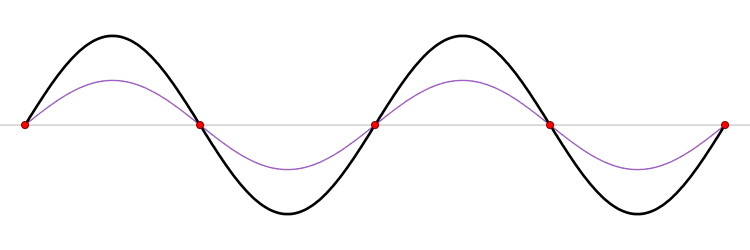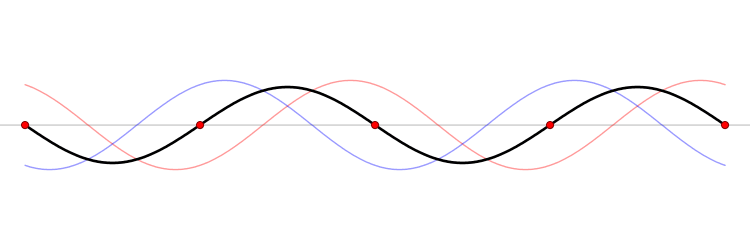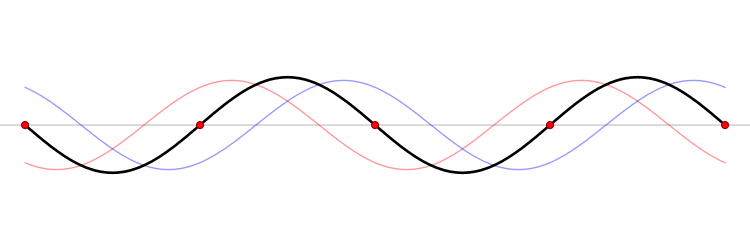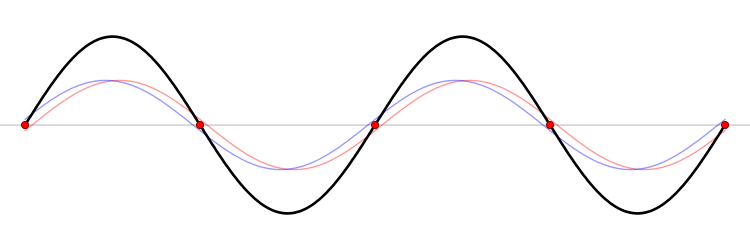
















![{\displaystyle s(t)=A_{c}[1+k_{a}m(t)]cos(2\pi f_{c}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54301e2b46261aa7df806170a41883492c56cf0)
Comentários
Postar um comentário